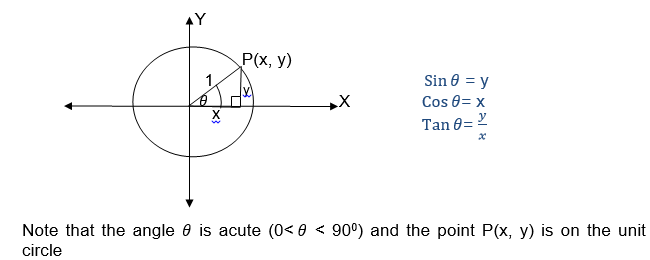
TRIGONOMETRY
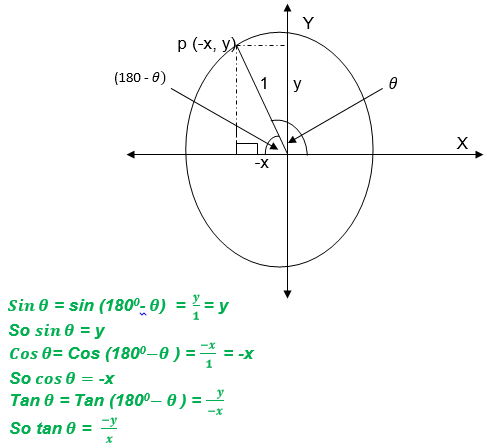
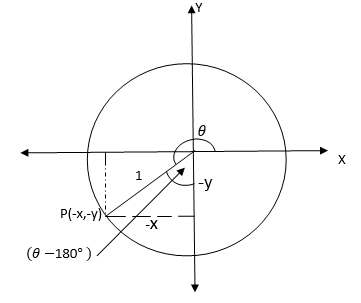
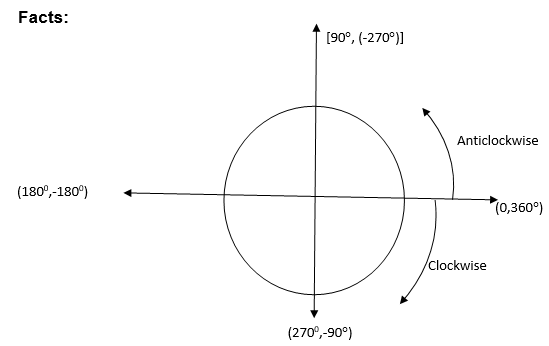
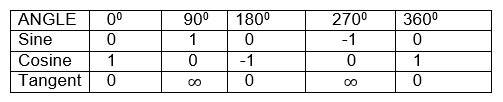
If θis a reflex angle (1800< θ<270 style="box-sizing: border-box;" sup="">0
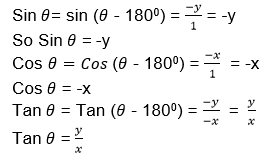
If θis a reflex angle (2700< θ< 3600), then the trigonometrical ratios are the same as that of 3600 -θ
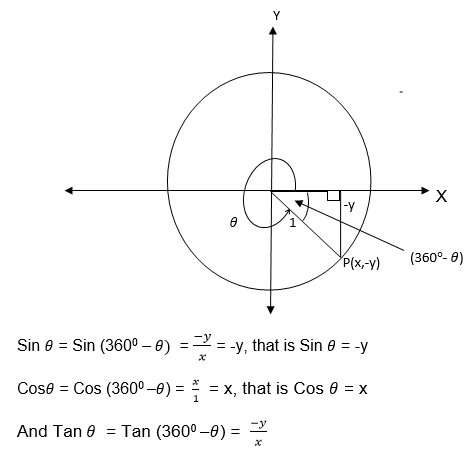
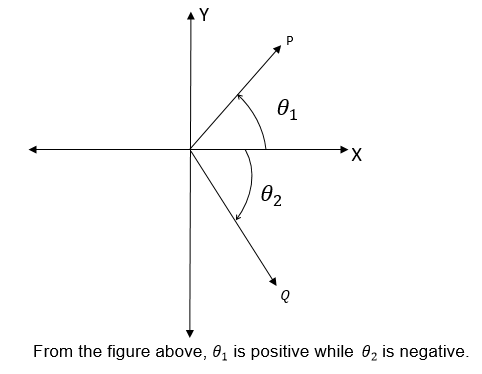
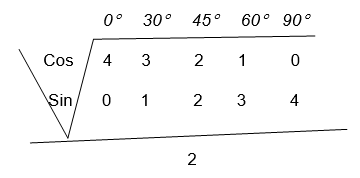
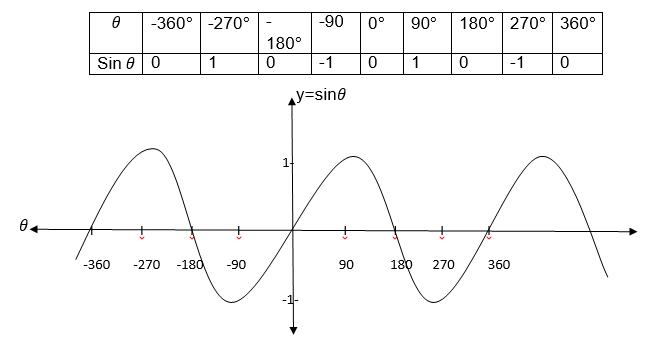
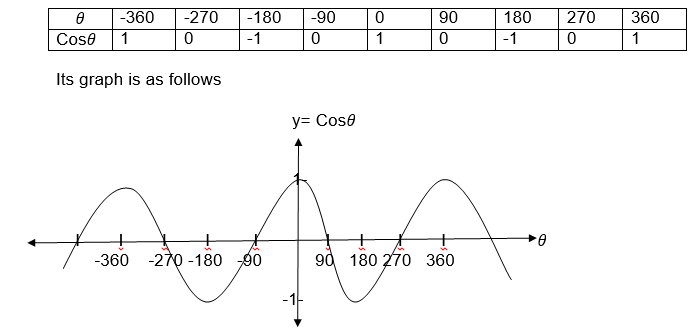
We have seen that trigonometrical ratios are positive or negative depending on the size of the angle and the quadrant in which it is found.
The result can be summarized by using the following diagram.
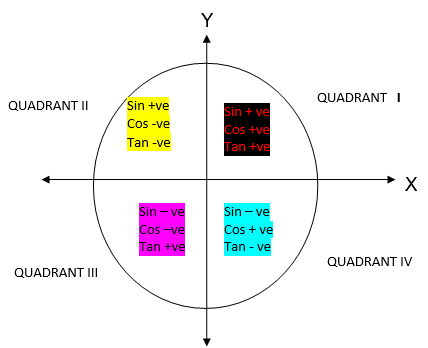
Trigonometric Ratios to Solve Problems in Daily Life
Apply trigonometric ratios to solve problems in daily life
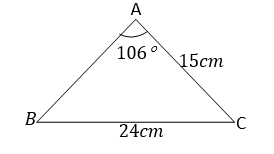
Example 1
Write the signs of the following ratios
- Sin 1700
- Cos 2400
- Tan 3100
- sin 300
Solution
a)Sin 1700
Since 1700 is in the second quadrant, then Sin 1700 = Sin (1800-1700) = Sin 100
∴Sin 1700 = Sin 100
b) Cos 2400 = -Cos (2400-1800)= -Cos 600
Therefore Cos 2400= -Cos 600
c) Tan 3100 = -Tan (3600-3100) = - Tan 500
Therefore Tan 3100= -Tan 500
d) Sin 3000= -sin (3600-3000) = -sin 600
Therefore sin 3000= - Sin 600
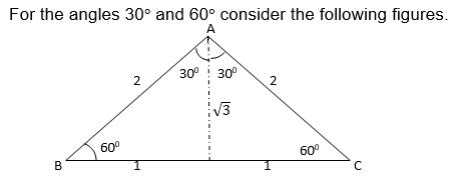
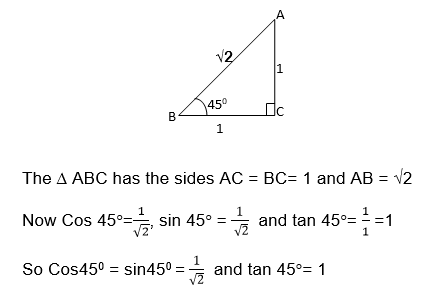
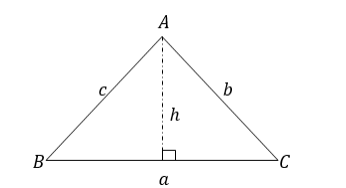
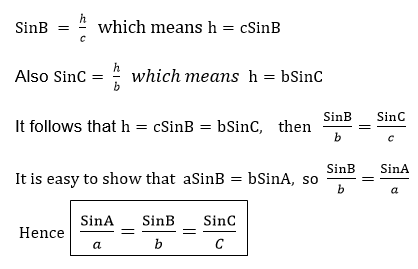
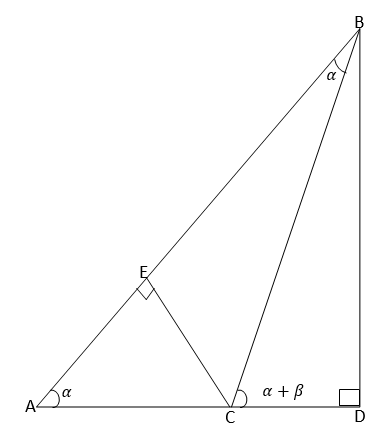
Relationship between Trigonometrical ratios
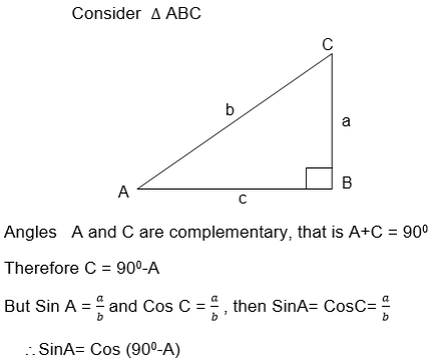
The above relationship shows that the Sine of angle is equal to the cosine of its complement.
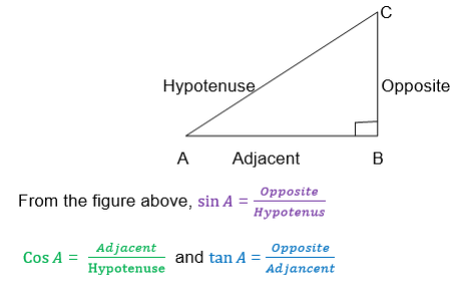
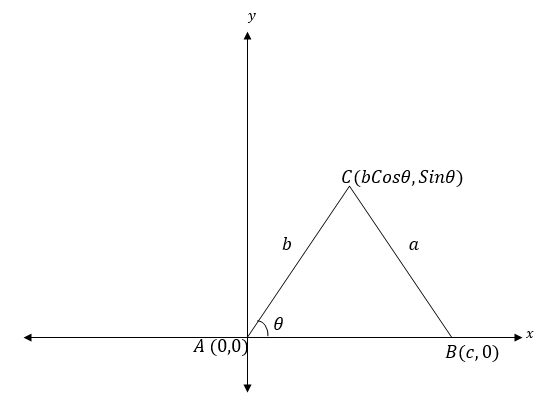
Also from the triangle ABC above

Again using the ΔABC
b2 = a2+c2 (Pythagoras theorem)
And
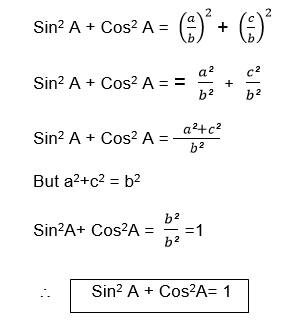
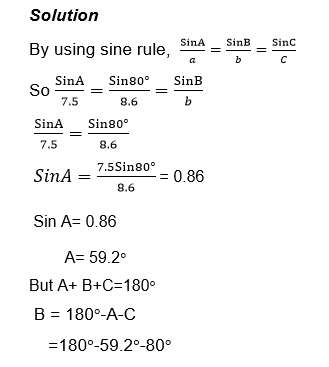
Example 2
Given thatA is an acute angle and Cos A= 0.8, find
- Sin A
- tan A.

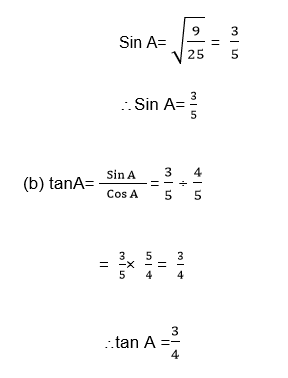
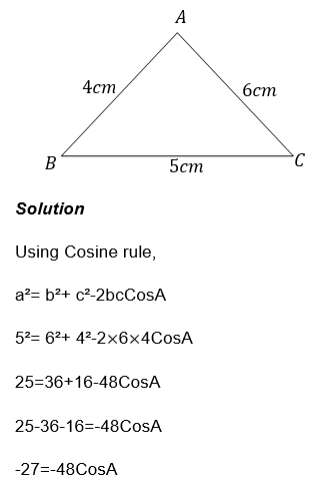
Example 3
If A and B are complementary angles,
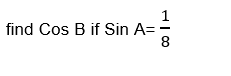
Solution
If A and B are complementary angle
Then Sin A = Cos B and Sin B = Cos A
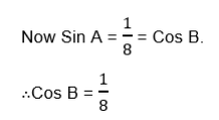
Example 4
Given that θand βare acute angles such that θ+ β= 900 and Sinθ= 0.6, find tanβ
Solution

Exercise 1
- READ TOPIC 6: Vectors


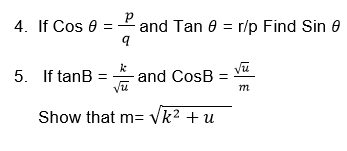


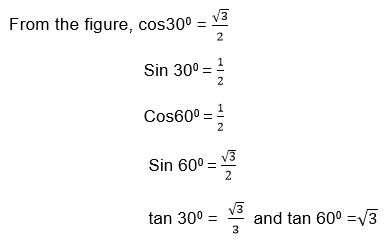



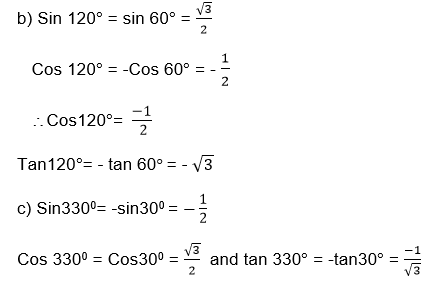



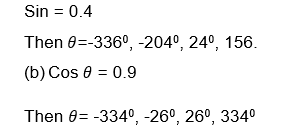
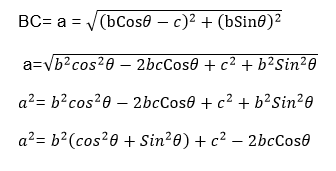

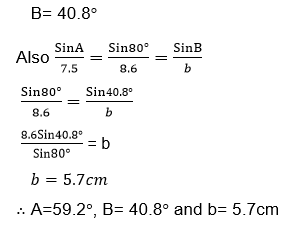

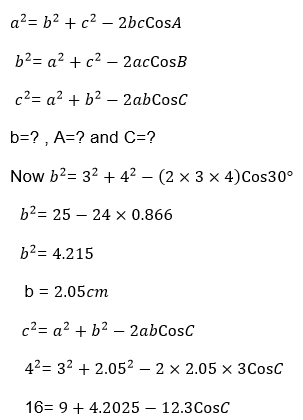
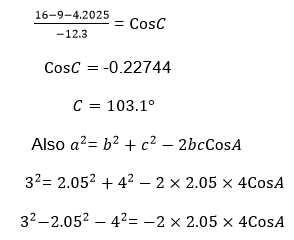
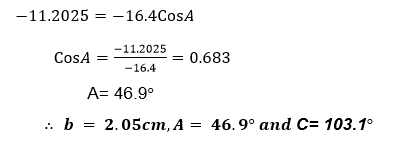

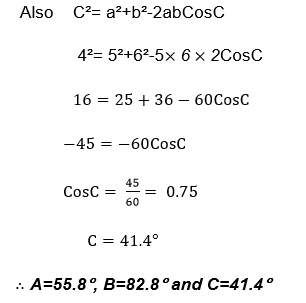



This is the good for all form four students
ReplyDelete