ALGEBRA
An algebraic expression – is a collection of numbers, variables, operators and grouping symbols.Variables - are letters used to represent one or more numbers
Algebraic Operations
Symbols to form Algebraic Expressions
Use symbols to form algebraic expressions
The parts of an expression collected together are called terms
Example
- x + 2x – are called like terms because they have the same variables
- 5x +9y – are called unlike terms because they have different variables
An algebraic expression can be evaluated by replacing or substituting the numbers in the variables
Example 1
Evaluate the expressions below, given that x = 2 and y = 3
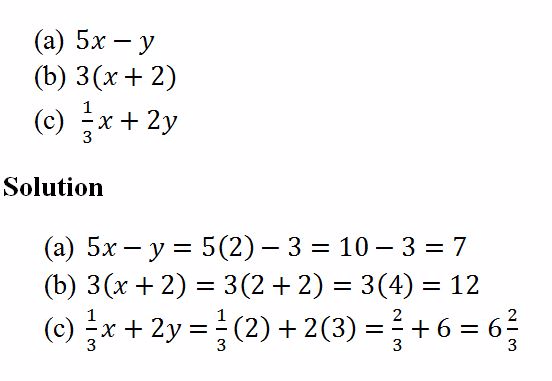
Example 2
Evaluate the expressions below, given that m = 1 and n = - 2
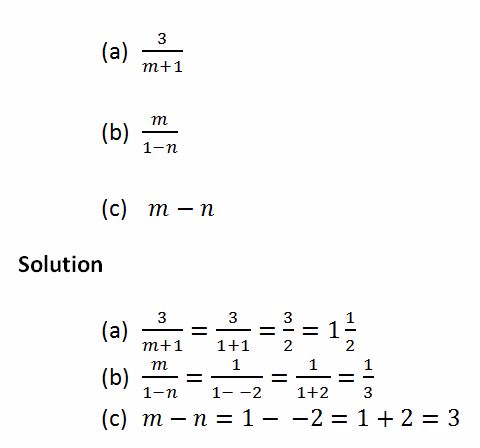
An expression can also be made from word problems by using letters and numbers
Example 3
A rectangle is 5 cm long and w cm wide. What is its area?
Solution
Let the area be A.
Then
A = length× widith
A = 5w cm2
Simplifying Algebraic Expressions
Simplify algebraic expressions
Algebraic expressions can be simplified by addition, subtraction, multiplication and division
Addition and subtraction of algebraic expression is done by adding or subtracting the coefficients of the like terms or letters
Coefficient of the letter – is the number multiplying the letter
Multiplication and division of algebraic expression is done on the coefficients of both like and unlike terms or letters
Example 4
Simplify the expressions below
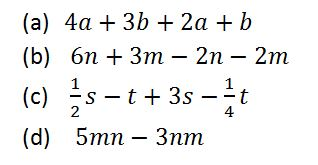
Solution
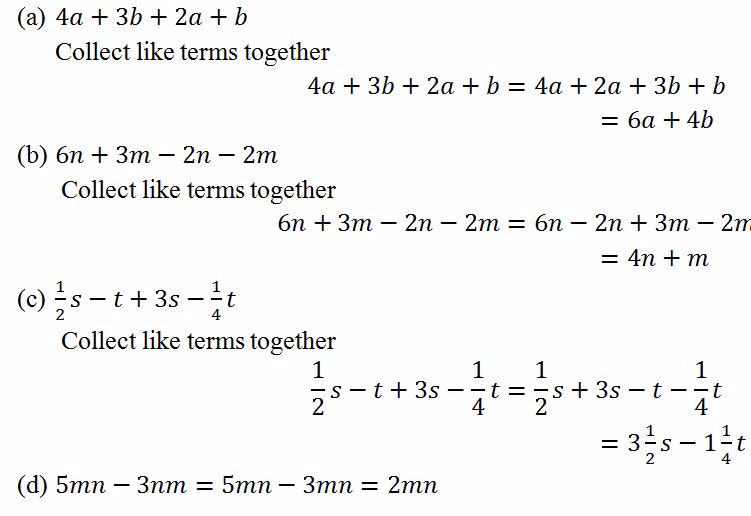
Equations with One Unknown
An equation – is a statement that two expressions are equal
An Equation with One Unknown
Solve an equation with one unknown
An equation can have one variable (unknown) on one side or two variables on both sides.
When you shift a number or term from one side of equation to another, its sign changes
- If it is positive, it becomes negative
- If it is negative, it becomes positive
Example 5
Solve the following equations
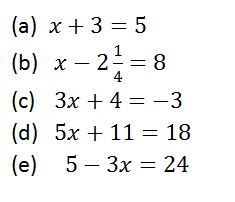
Solution
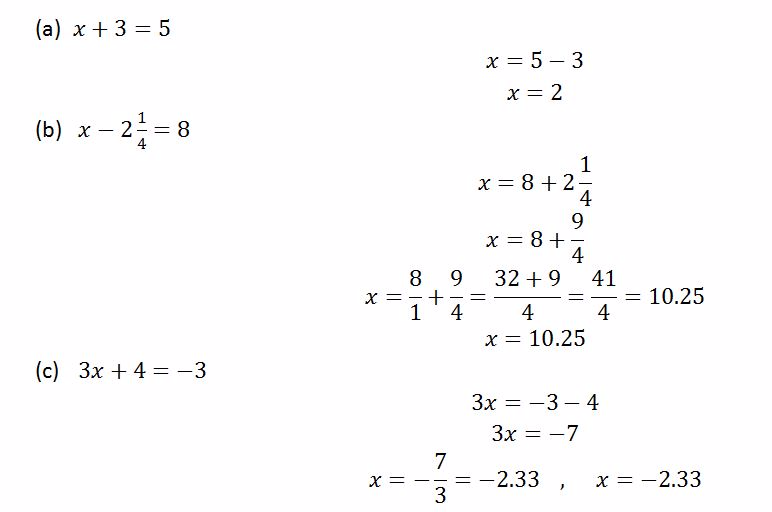
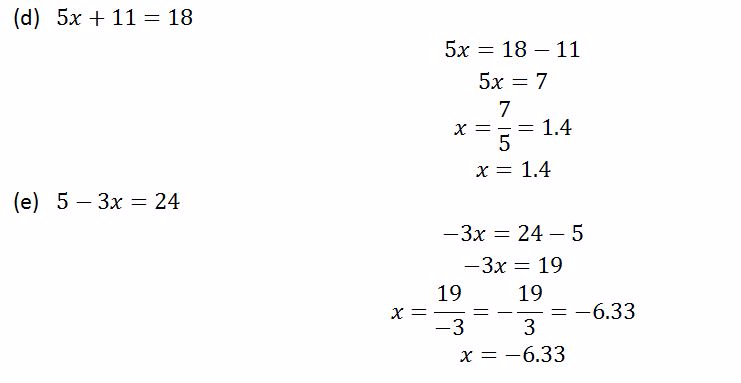
An Equation from Word Problems
Form and solve an equation from word problems
Some word problems can be solved by using equations as shown in the below examples
Example 6
Naomi is 5 years young than Mariana. The total of their ages 33 years. How old is Mariana?
Solution
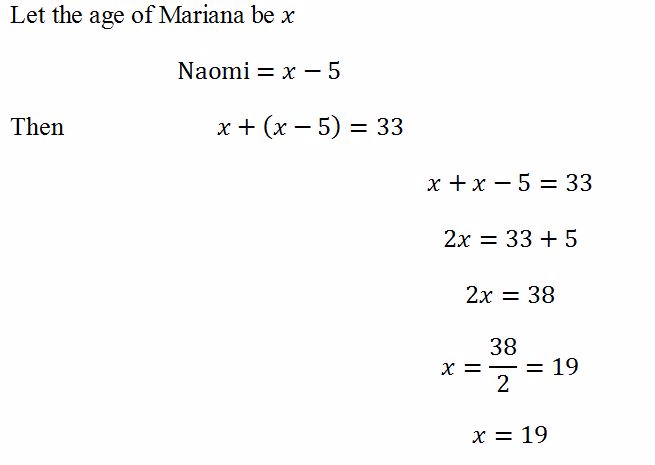
Mariana is 19 years
Equations with Two Unknowns
Simultaneous Equations
Solve simultaneous equations
Simultaneous equations – are groups of equations containing multiple variables
Example 7
Examples of simultaneous equation
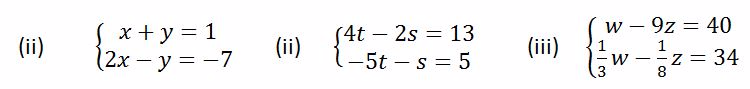
A simultaneous equation can be solved by using two methods:
- Elimination method
- Substitution method
ELIMINATION METHOD
STEPS
- Choose a variable to eliminatee.g x or y
- Make sure that the letter to be eliminated has the same coefficient in both equations and if not, multiply the equations with appropriate numbers that will give the letter to be eliminated the same coefficient in both equations
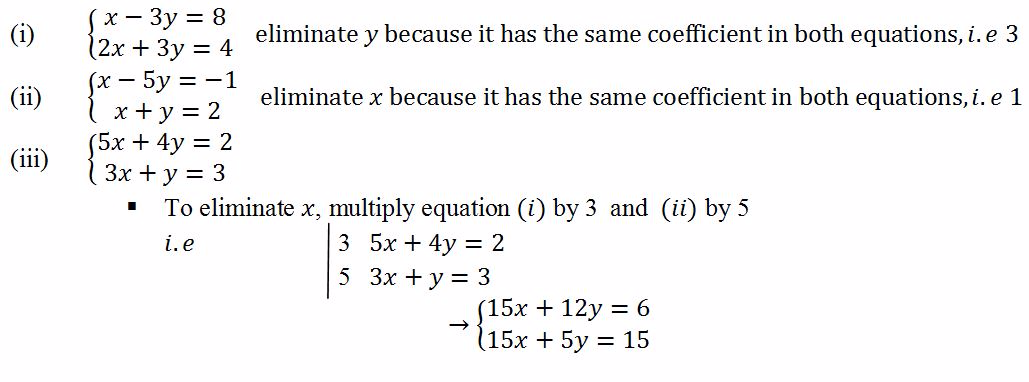
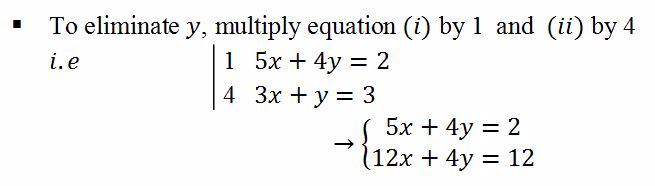
- If the signs of the letter to be eliminated are the same, subtract the equations
- If the signs of the letter to be eliminated are different, add the equations
Example 8
Solve the following simultaneous equations by elimination method
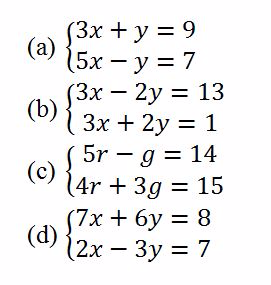
Solution
- Eliminate y
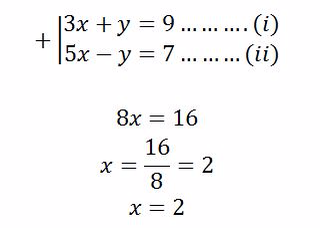
To find y put x = 2 in either equation (i) or (ii)
From equation (i)

(b)Eliminate x
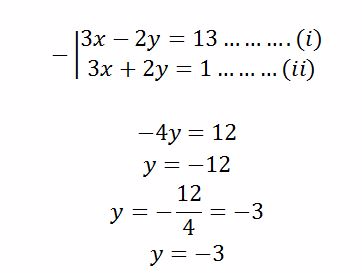
In order to find y, put x = 2 in either equation (i) or (ii)
From equation (ii)
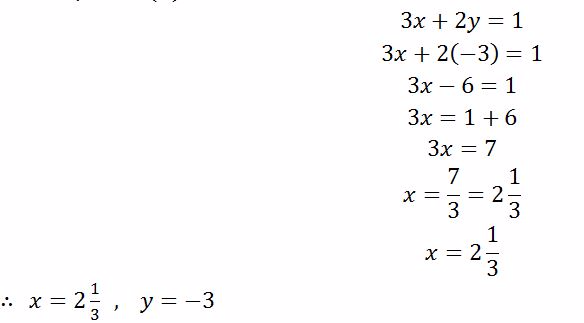
(c) Given
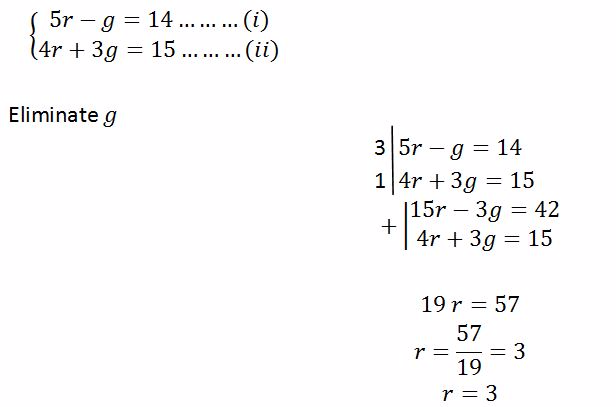
To find g put r = 3 in either equation (i) or (ii)
From equation (i)
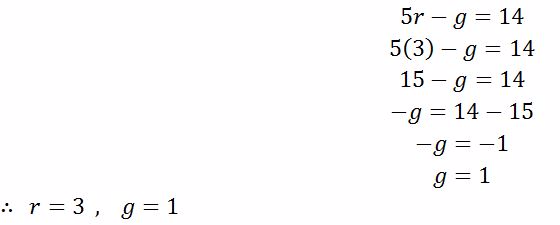
(d) Given
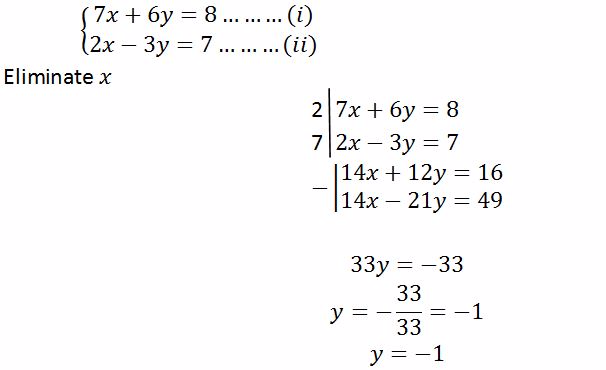
To find x, put y = - 1 in either equation(i) or (ii)
From equation (ii)
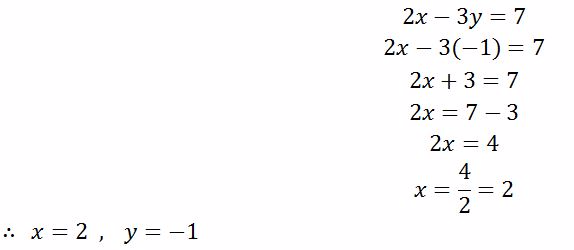
BY SUBSTITUTION
STEPS
- Make the subject one letter in one of the two equation given
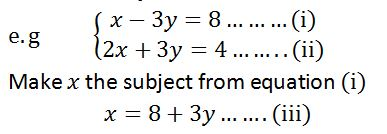
- Substitute the letter in the remaining equation and proceed as in case of elimination
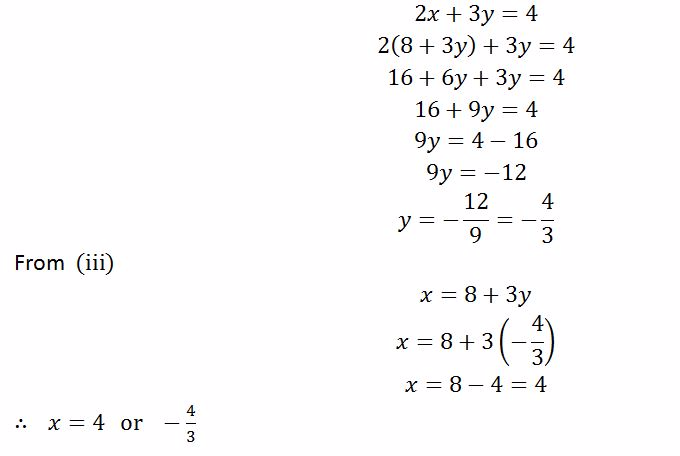
Example 9
Solve the following simultaneous equations by substitution method
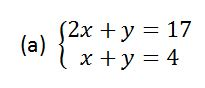
Solution
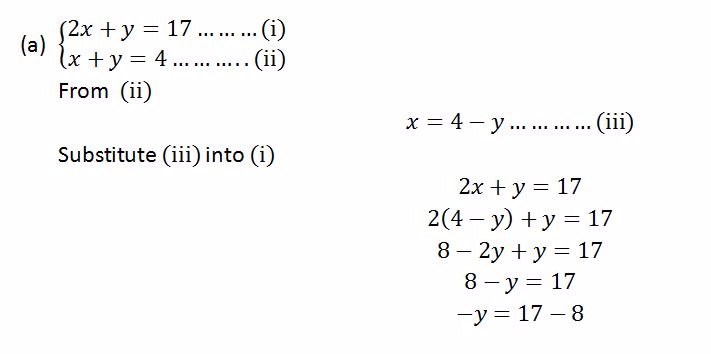
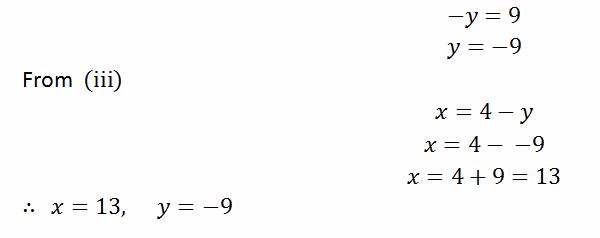
Linear Simultaneous Equations from Practical Situations
Solve linear simultaneous equations from practical situations
Simultaneous equations can be used to solve problems in real life involving two variables
Example 10
If 3 Mathematics books and 4 English books weighs 24 kg and 5 Mathematics books and 2 English books weighs 20 kg, find the weight of one Mathematics book and one English book.
Solution
Let the weight of one Mathematics book = x and
Let the weight of one English book = y
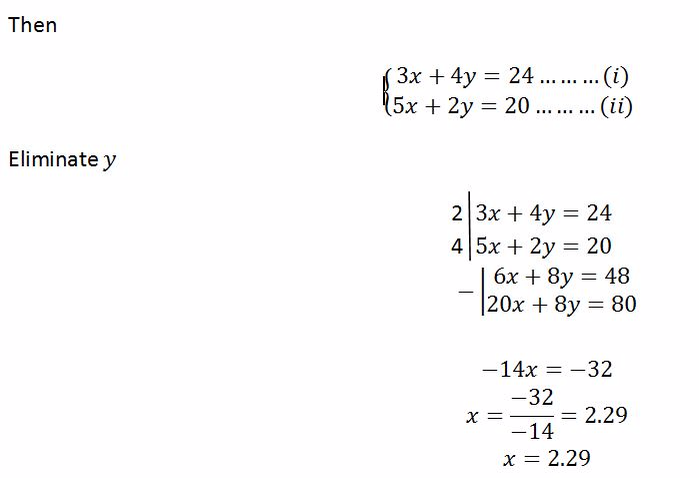
To find y, put x = 2.29 in either equation (i) or (ii)
From equation(i).
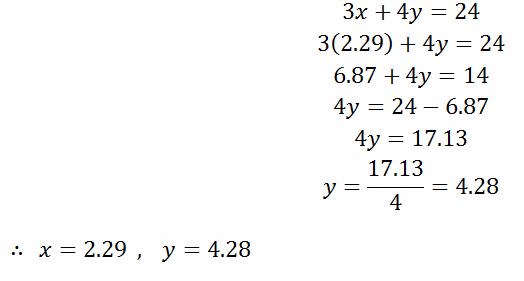
Inequalities
An inequality – is a mathematical statement containing two expressions which are not equal. One expression may be less or greater than the other.The expressions are connected by the inequality symbols<,>,≤ or≥.Where< = less than,> = greater than,≤ = less or equal and ≥ = greater or equal.
Linear Inequalities with One Unknown
Solve linear inequalities in one unknown
An inequality can be solved by collecting like terms on one side.Addition and subtraction of the terms in the inequality does not change the direction of the inequality.Multiplication and division of the sides of the inequality by a positive number does not change the direction of the inequality.But multiplication and division of the sides of the inequality by a negative number changes the direction of the inequality
Example 11
Solve the following inequalities

Solution
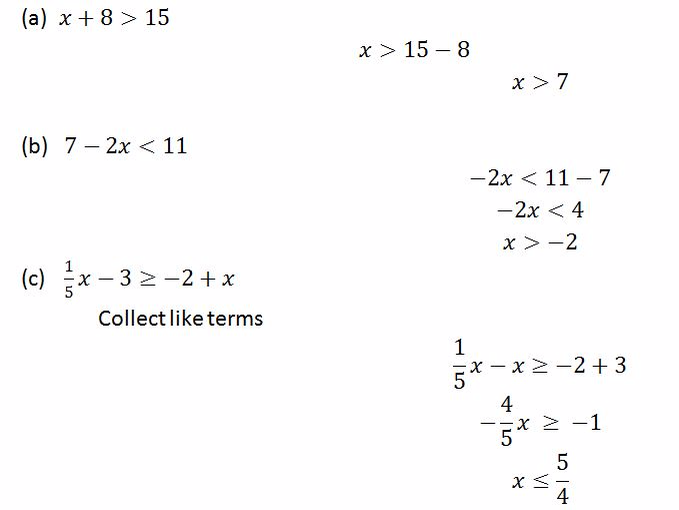
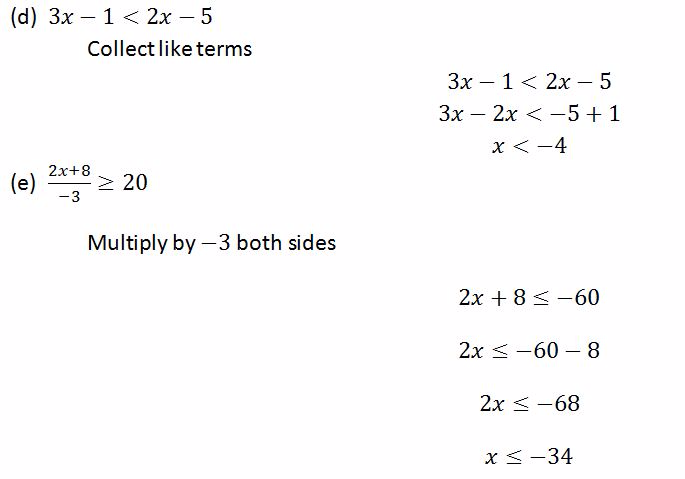
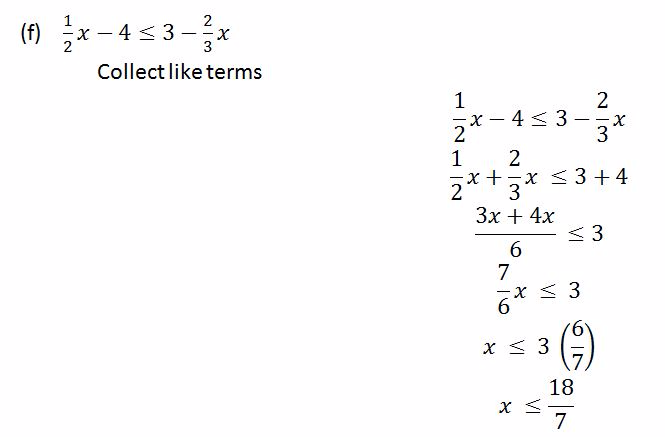
Linear Inequalities from Practical Situations
Form linear inequalities from practical situations
To represent an inequality on a number line, the following are important to be considered:
- The endpoint which is not included is marked with an empty circle
- The endpoint which is included is marked with a solid circle
Example 12

Compound statement – is a statement made up of two or more inequalities
Example 13
Solve the following compound inequalities and represent the answer on the number line
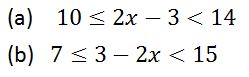
Solution

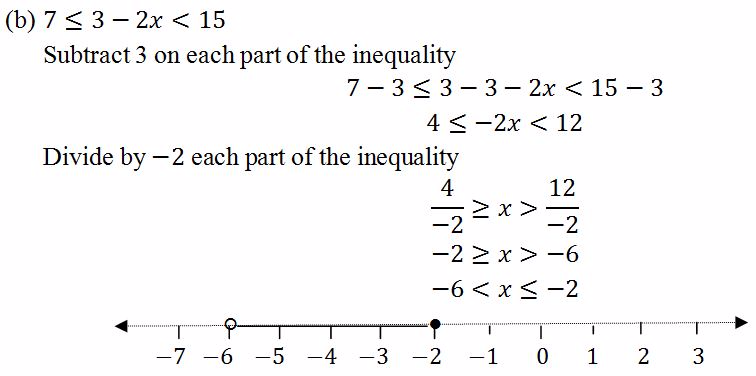
- READ TOPIC 8: Numbers (II)

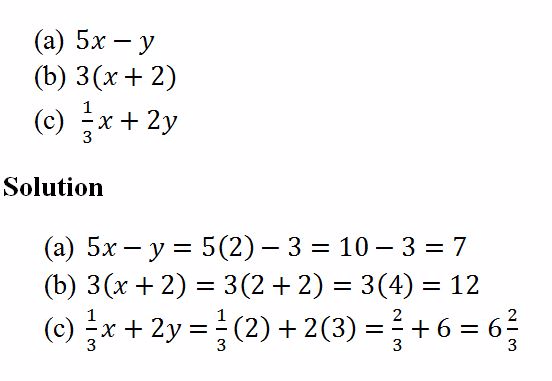

Thank you so much... At last i found what i was looking for
ReplyDeleteThank you so much for your good notes
ReplyDelete